In this post we are going to look at sports betting and how to make guarenteed money. Let’s take the example of football. For each match, there is a home team who hosts the match in their stadium and an away team. There are three outcomes to each match, home win (away lose), home lose (away win) and a draw.
The bookie provides odds on each outcome. This is typically quoted as 3:2, which stands for bet £2 and win £3 + get back the £2 original bet. I find this incredible unintuitive so in this post I will use the convention of saying the odds are 1.5, which means if you bet £1 you get £1.5 back from the bookie (£0.50 + the original £1 bet).
Suppose that \(\mathbf{d} = (d_1, d_2, d_3) = (d_{\text{win}}, d_{\text{lose}}, d_{\text{draw}})\) be the odds that one bookmaker provides on the home team winning, losing and drawing respectively. There is an arbitrage opertunity if we can place bets across the three events such that we make money no matter which event occurs. So two questions, when does this happen and how can I place the bets when it happens?

Let’s do this!
Let \(\mathbf{b}=(b_1, b_2, b_3)\) be some bets on the three events, define the worst case outcome as \[ W_\mathbf d(\mathbf b) = \min_{i=1, 2, 3}b_i d_i. \] This is the least amount of money made between the three outcomes. In order for the bet to make money no matter what, it must be the case that \[ W_\mathbf d(\mathbf b) > \mathbf b^t \mathbf 1 = b_1 + b_2 + b_3 \] since \(b_1+b_2+b_3\) is the total amount of money placed as bets.
So how can be maximise \(W_\mathbf d(\mathbf b)\) over \(\mathbf b \geq 0\) such that the total size of the bet \(b_1 + b_2 + b_3 = 1\)? First notice that if \(\mathbf{\hat b}\) maximises \(W_\mathbf d\), then it must be case that \(\hat b_1d_1 = \hat b_2d_2 b =\hat b_3d_3\). If this wasn’t true then we can shift some of the bet from the best case senario to the worst case to increase \(W_\mathbf d\). This means that \[ \hat b_i =\frac{c}{d_i}. \] maximises \(W_\mathbf d\) for some \(c>0\). Since the total size of the bet is fixed, it must be the case that \[ c = (d_1^{-1} + d_2^{-1} + d_3^{-1})^{-1}. \]
Now we can easily see the arbitrage condition which happens whenever \[ (\hat b_i d_i)^{-1} = d_1^{-1} + d_2^{-1} + d_3^{-1} < 1 \qquad \text{ for all } i=1,2,3. \]
Alright, I can hear you screaming that no bookie is going to let you have an arbitrage opertunity, so what’s the point? Well the idea is if we know odds from several bookies, we can take the maximum odds for each event and think of these odds as a bookmaker. This means that we can place bets across multiple bookies and make money no matter what happens if \[ \begin{aligned} &(\max_i\{\text{home-win odds of bookie } i\})^{-1} + \quad &\\ &(\max_i\{\text{home-lose odds of bookie } i\})^{-1} +\quad& \\ &(\max_i\{\text{draw odds of bookie } i\})^{-1} &< 1. \end{aligned} \]

Time to make some money.
I have gathered some bookmaker odds from https://the-odds-api.com/.
library(tidyverse)
df <- read_csv('../../data/arb/arbs.csv')
df %>%
select(sport, home, away, profit_percent) %>%
mutate(profit_percent = sprintf('%.2f%%', profit_percent)) %>%
rename(profit=profit_percent) %>%
DT::datatable()The size of the arbitrage opertunities are actually quite small (which is what you would expect).
df %>%
ggplot(aes(profit_percent / 100, fill=sport)) +
geom_histogram(bins=10, position='stack') +
scale_x_continuous(labels=scales::percent) +
labs(title='Size of arbitrage opertunities',
x='Arbitrage return',
y='Number of opertunities',
fill='')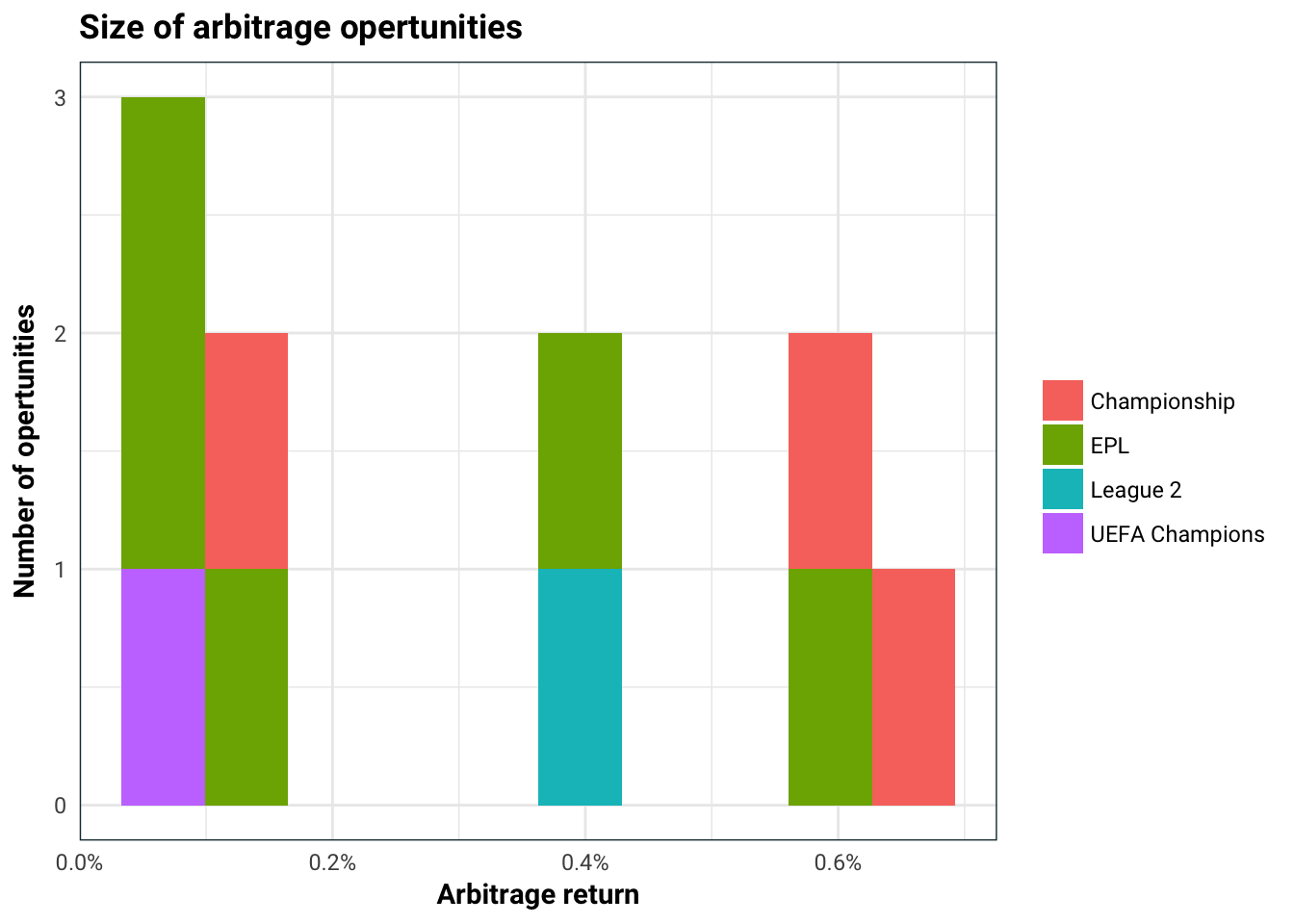
Here is the biggest arbitrage bet you can make.
df %>%
slice(1) %>%
select(home_win_site, home_odds, away_win_site, away_odds, draw_site, draw_odds)#> # A tibble: 1 x 6
#> home_win_site home_odds away_win_site away_odds draw_site draw_odds
#> <chr> <dbl> <chr> <dbl> <chr> <dbl>
#> 1 William Hill 1.78 Sky Bet 5.5 1xBet 4