Welcome to part two of the two part series on a crash course into state of the art natural language processing. This part is going to go through the transformer architecture from Attention Is All You Need. If you haven’t done so already, read the first part which introduces attention mechanisms. This post is all about transformers and assumes you know attention mechanisms.

Let’s being by recalling the definition of an attention mechanism from part-one in a slightly more general way: $$ \begin{aligned} K_w = u_K \cdot W_K, \quad u_K\in \mathbb{R}^{d_{\text{embedding}}}, W_K \in \mathbb{R}^{d_{\text{embedding}}, d_K}\\ Q_w = u_Q \cdot W_Q, \quad u_Q\in \mathbb{R}^{d_{\text{embedding}}}, W_Q \in \mathbb{R}^{d_{\text{embedding}}, d_K}\\ V_w = u_V \cdot V_K, \quad u_V\in \mathbb{R}^{d_{\text{embedding}}}, V_K \in \mathbb{R}^{d_{\text{embedding}}, d_V}. \end{aligned} $$ and $$ \text{Attention}(Q, K, V) = \text{masked-softmax}\left(\frac{QK^t}{\sqrt d_k}\right) V. $$ where in masked-softmax, we use a mask to determine the entries that are forced to have zero output.
The difference to the first post here is that the vector used in the key, query and value is allowed to be different. Secondly, we apply a mask to the weight (similar to how we did next word predictions in the previous post). This mask will allow us to vectorise everything. Third, there is an additional linear model at the end of the attention mechanism. I’m not quite convinced that this really makes a difference, but it’s in the paper.
import torch
torch.manual_seed(1234)
from torch import nn
class Attention(nn.Module):
def __init__(self, embed_dim, d_k, d_v):
super().__init__()
self.W_K = nn.Parameter(torch.randn((embed_dim, d_k)) * .01)
self.W_Q = nn.Parameter(torch.randn((embed_dim, d_k)) * .01)
self.W_V = nn.Parameter(torch.randn((embed_dim, d_k)) * .01)
self.scaling = torch.Tensor(np.array(1 / np.sqrt(d_k)))
def _weight_value(self, Q_vec, K_vec, V_vec, mask):
K = K_vec @ self.W_K
Q = Q_vec @ self.W_Q
V = V_vec @ self.W_V
weight = self.scaling * Q @ K.transpose(0, 1)
exp_weight = torch.exp(torch.clamp(weight, max=25)) * mask.float()
attn = exp_weight / (torch.sum(exp_weight, dim=1, keepdim=True) + 1e-5)
return attn, V
def forward(self, Q_vec, K_vec, V_vec, mask):
weight, V = self._weight_value(Q_vec, K_vec, V_vec, mask)
return weight @ V
class MultiHeadAttention(nn.Module):
def __init__(self, embed_dim, d_k, d_v, num_heads):
super().__init__()
self.attns = nn.ModuleList([Attention(embed_dim, d_k, d_v) for _ in range(num_heads)])
self.linear = nn.Linear(num_heads * d_v, embed_dim)
def forward(self, Q_vec, K_vec, V_vec, mask):
results = [attn(Q_vec, K_vec, V_vec, mask) for attn in self.attns]
return self.linear(torch.cat(results, dim=1))
The goal of this post is to understand and construct the network:
Let’s walk through this image step by step. The goal here is to translate a sentence from one language (inputs) to an other language (outputs). For example, here is an input and output pair:
encoder_input = 'dogs are awesome <pad> <eos>'
decoder_input = '<pad> hunde sind wunderbar <eos>'
decoder_output = 'hunde sind wunderbar <pad> <eos>'
We will train the network by feeding it encoder_input and decoder_input and asking it to predict decoder_output. The encoder input is padded using the <pad> tag and <eos> denotes the end of sentence. These both need to be masked. For the decoder, the input needs to be masked in a similar way to how we did it for the next word prediction: if the decoder is working on translating word i, then it should have access to all the words in decoder_input[j] for j<=i. Notice that decoder_input is shifted, meaning that for example, when trying to decode the word dogs it only has access to the words dogs and <pad>. This means that the network doesn’t have any look-ahead bias.
First, just take a look at the left network in the above image, which is called the encoder. It takes in the language to be translated, as input and numerically encodes it (we can use nn.Embedding in pytorch). This simply does what we did in the last post, except instead of matrix multiplication it just looks up the index. It will try to learn a matrix $M \in \mathbb {R}^{d_{vocab} \times d_{embed}}$ and map $f(i) = M[i, :]$ each number to the row corresponding to that index.
The attention mechanism doesn’t really care about the order of the words. To remedy this, after the nn.Embedding layer is applied, we add a vector pos:
import matplotlib.pyplot as plt
plt.style.use('ggplot')
%matplotlib inline
import seaborn as sns
import numpy as np
def pos_fun(n_dims, n_embed):
result = np.zeros((n_dims, n_embed))
for i in range(n_embed):
if i % 2 == 0:
result[:, i] = [np.sin(pos / np.power(10000, i / n_embed))
for pos in range(n_dims)]
else:
result[:, i] = [np.cos(pos / np.power(10000, (i-1) / n_embed))
for pos in range(n_dims)]
return result
fig, ax = plt.subplots(figsize=(8, 7))
sns.heatmap(pos_fun(100, 100), ax=ax, cmap='bwr_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
ax.set_title('Positional encoding')
fig.show()
/Users/bati/anaconda3/lib/python3.6/site-packages/matplotlib/figure.py:418: UserWarning: matplotlib is currently using a non-GUI backend, so cannot show the figure
"matplotlib is currently using a non-GUI backend, "
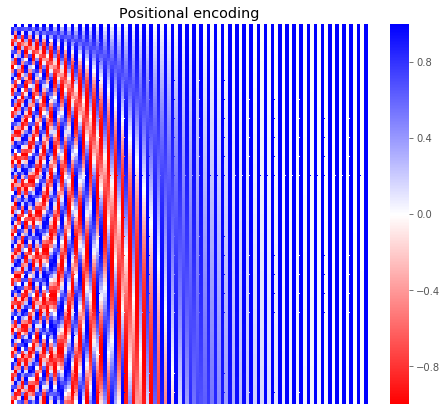
Why is it done this way? I don’t really have an answer to that other than it works. The authors say:
We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k, PE_{pos+k} can be represented as a linear function of PE_{pos}.
So the full code for the input embedding looks like this:
class InputEmbedding(nn.Module):
def __init__(self, n_words, n_embed, max_len=100):
super().__init__()
self.n_embed = n_embed
self.embedding = nn.Embedding(n_words, n_embed)
self.position_emb = nn.Embedding.from_pretrained(
torch.Tensor(pos_fun(max_len, n_embed)), freeze=True)
def forward(self, x):
idx = torch.arange(0, len(x), device=x.device, dtype=x.dtype)
return self.embedding(x) + self.position_emb(idx)
Next there is a residual connection, which means that the embedding is both fed to the attention mechanism and also a copy of it also is added to the output of the mechanism. The whole thing is then layer normalised and fed to a feed forward network. Again the output of the feed-forward network has a residual connection and layer normalisation. This structure is repeated 3 times in the paper. I also added the parameters that the paper uses as defaults.
class EncoderLayer(nn.Module):
def __init__(self,
embed_dim=64 * 8,
d_k=64, d_v=64,
num_heads=8):
super().__init__()
self.attn = MultiHeadAttention(embed_dim, d_k, d_v, num_heads)
self.ffn = nn.Linear(embed_dim, embed_dim)
self.ln1 = nn.LayerNorm(embed_dim)
self.ln2 = nn.LayerNorm(embed_dim)
def forward(self, x, mask):
attn_out = self.attn(x, x, x, mask)
ln1_out = self.ln1(attn_out + x)
ffn_out = nn.functional.relu(self.ffn(ln1_out))
return self.ln2(ffn_out + ln1_out)
class Encoder(nn.Module):
def __init__(self, n_words, embed_dim=512, n_layers=3):
super().__init__()
self.input_enc = InputEmbedding(n_words, embed_dim)
self.layers = nn.ModuleList([EncoderLayer() for _ in range(n_layers)])
def forward(self, x, mask):
out = self.input_enc(x)
for layer in self.layers:
out = layer(out, mask)
return out
OK, so that covers the left hand side of the network. The right side is pretty similar and is the decoder. As it’s input, it takes the translation that was made so far, and outputs the next word. The only real difference to the encoder is that it uses the output of the encoder in the second multi-head attention. This allows it to use the information from the encoding to determine which previously translated words to pay attention to when translating the next word.
class DecoderLayer(nn.Module):
def __init__(self,
embed_dim=64 * 8,
d_k=64, d_v=64,
num_heads=8):
super().__init__()
self.attn1 = MultiHeadAttention(embed_dim, d_k, d_v, num_heads)
self.attn2 = MultiHeadAttention(embed_dim, d_k, d_v, num_heads)
self.ffn = nn.Linear(embed_dim, embed_dim)
self.ln1 = nn.LayerNorm(embed_dim)
self.ln2 = nn.LayerNorm(embed_dim)
self.ln3 = nn.LayerNorm(embed_dim)
def forward(self, x, encoder_output, mask=None):
attn1_out = self.attn1(x, x, x, mask)
ln1_out = self.ln1(attn1_out + x)
attn2_out = self.attn2(ln1_out,
encoder_output,
encoder_output,
mask)
ln2_out = self.ln2(attn2_out + ln1_out)
ffn_out = nn.functional.relu(self.ffn(ln2_out))
return self.ln3(ffn_out + ln2_out)
class Decoder(nn.Module):
def __init__(self, n_words, embed_dim=512, n_layers=3):
super().__init__()
self.input_enc = InputEmbedding(n_words, embed_dim)
self.layers = nn.ModuleList([DecoderLayer() for _ in range(n_layers)])
def forward(self, x, encoder_output, mask):
out = self.input_enc(x)
for layer in self.layers:
out = layer(out, encoder_output, mask)
return out
With all encoder and decoder ready, we can finally combine it together to get the transformer:
class Transformer(nn.Module):
def __init__(self, n_base_words, n_target_words, embed_dim=512):
super().__init__()
self.encoder = Encoder(n_base_words, embed_dim=embed_dim)
self.decoder = Decoder(n_target_words, embed_dim=embed_dim)
self.linear = nn.Linear(embed_dim, n_target_words)
def forward(self,
encoder_input,
decoder_input,
encoder_mask,
decoder_mask):
encoder_out = self.encoder(encoder_input, encoder_mask)
decoder_out = self.decoder(decoder_input, encoder_out, decoder_mask)
return torch.softmax(self.linear(decoder_out), dim=0)
Finally, a little overkill, but I also added some classes to do the annoying string to numerical encodings.
import string
import pandas as pd
class WordNumerics(object):
def __init__(self, list_of_sentences):
self.words = set().union(*list_of_sentences)
# Make sure <eos> = 0 and <pad> = 1
self.words.remove('<pad>')
self.words.remove('<eos>')
self.words = ['<eos>', '<pad>'] + list(self.words)
self.word2num = {w: i for i, w in enumerate(self.words)}
self.num2word = {i: w for i, w in enumerate(self.words)}
def numeric(self, sentence):
return np.array([self.word2num[x] for x in sentence])
def string(self, vec):
return ' '.join([self.num2word[x] for x in vec])
def one_hot(self, vec):
n_words = len(self.words)
result = np.zeros((len(vec), n_words))
for i, val in enumerate(vec):
result[i, val] = 1
return result
def __len__(self):
return len(self.words)
class HandleStrings(object):
def __init__(self, pairs_of_sentences):
pairs_of_sentences = [(self._clean(x), self._clean(y))
for x, y in pairs_of_sentences]
self.text = [self._make_triplet(*x) for x in pairs_of_sentences]
self.base = WordNumerics([x[0] for x in self.text])
self.target = WordNumerics([x[1] for x in self.text])
self.numeric = [(self.base.numeric(x), self.target.numeric(y), self.target.numeric(z))
for x,y,z in self.text]
self.enc_in = [x for x, _, _ in self.numeric]
self.dec_in = [x for _, x, _ in self.numeric]
self.dec_out = [x for _, _, x in self.numeric]
self.data = self._make_data()
def _make_data(self):
torch_fun = [torch.LongTensor] * 2 + [torch.Tensor] * 3
data_combined = list()
for i in range(len(self.enc_in)):
data = [self.enc_in[i],
self.dec_in[i],
self.target.one_hot(self.dec_out[i]),
self.encoder_mask(self.enc_in[i]),
self.decoder_mask(self.dec_in[i])]
data = [f(x) for f, x in zip(torch_fun, data)]
data_combined.append(tuple(data))
return data_combined
def _clean(self, s):
s = s.lower()
translator = s.maketrans('', '', string.punctuation)
return s.translate(translator)
def _make_triplet(self, base, target):
base, target = base.split(' '), target.split(' ')
diff = len(base) - len(target)
if diff > 0:
target += ['<pad>'] * diff
elif diff < 0:
base += ['<pad>'] * (-diff)
return (base + ['<pad>', '<eos>'],
['<pad>'] + target + ['<eos>'],
target + ['<pad>', '<eos>'])
def make_mask(self, vec):
n = len(vec)
mask = np.ones((n, n))
padding = (vec == 1) | (vec == 0)
mask[:, padding] = 0
return mask
def encoder_mask(self, vec):
return self.make_mask(vec)
def decoder_mask(self, vec):
n = len(vec)
look_ahead = np.tril(np.ones(n))
return self.make_mask(vec) * look_ahead
def set_device(self, device):
self.device = device
return self
def __len__(self):
return len(self.text)
def __getitem__(self, i):
return self.data[i]
def __setitem__(self, i, value):
self.data[i] = value
def to(self, *args, **kwargs):
self.data = [tuple([tensor.to(*args, **kwargs) for tensor in entry])
for entry in self.data]
return self
translations = [('Dogs are awesome.', 'Hunde sind wunderbar!')]
handler = HandleStrings(translations)
print('Example:')
display(translations[0])
enc_in_str, dec_in_str, dec_out_str = handler.text[0]
enc_in, dec_in, dec_out, enc_mask, dec_mask = handler[0]
print('Encoder input + mask:')
display(pd.Series(enc_in.detach().numpy(), index=enc_in_str))
display(pd.DataFrame(enc_mask.detach().numpy(), index=enc_in_str, columns=enc_in_str))
print('Decoder input + mask:')
display(pd.Series(dec_in.detach().numpy(), index=dec_in_str))
display(pd.DataFrame(dec_mask.detach().numpy(), index=enc_in_str, columns=dec_in_str))
print('Decoder target:')
display(pd.DataFrame(dec_out.detach().numpy(), index=dec_out_str, columns=handler.target.words))
Example:
('Dogs are awesome.', 'Hunde sind wunderbar!')
Encoder input + mask:
dogs 2
are 3
awesome 4
<pad> 1
<eos> 0
dtype: int64
| dogs | are | awesome | <pad> | <eos> | |
|---|---|---|---|---|---|
| dogs | 1.0 | 1.0 | 1.0 | 0.0 | 0.0 |
| are | 1.0 | 1.0 | 1.0 | 0.0 | 0.0 |
| awesome | 1.0 | 1.0 | 1.0 | 0.0 | 0.0 |
| <pad> | 1.0 | 1.0 | 1.0 | 0.0 | 0.0 |
| <eos> | 1.0 | 1.0 | 1.0 | 0.0 | 0.0 |
Decoder input + mask:
<pad> 1
hunde 4
sind 3
wunderbar 2
<eos> 0
dtype: int64
| <pad> | hunde | sind | wunderbar | <eos> | |
|---|---|---|---|---|---|
| dogs | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| are | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| awesome | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 |
| <pad> | 0.0 | 1.0 | 1.0 | 1.0 | 0.0 |
| <eos> | 0.0 | 1.0 | 1.0 | 1.0 | 0.0 |
Decoder target:
| <eos> | <pad> | wunderbar | sind | hunde | |
|---|---|---|---|---|---|
| hunde | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| sind | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| wunderbar | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| <pad> | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 |
| <eos> | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
When decoding the i-th word, the mask on the i-th row will be used, so for example, when the network tries to translate “are”, the only word in German that it can see is “hunde” as can be seen in the decoder mask. Now we can train the model on a few of my favourite quotes:
from tqdm import tqdm
from random import shuffle
translations = [
('I\'m Mr Meseeks, look at me', 'Ich bin Mr Meseeks, sieht mich an'),
('Nobody exists on purpose, nobody belongs anywhere, everybody is gonna die. Come watch TV?',
'Niemand gehört irgendwo hin, niemand existiert mit Absicht, wir alle werden sterben. Komm, Fernsehen gucken?“'),
('I am the one who knocks', 'ich bin derjenige der Knopft'),
('my cat\'s breath smells like catfood', 'der atem meiner katze riecht nach katzenfutter'),
('weaselling out of things is important to learn, it is what separates us from the animals, except the weasel',
'Sich irgendwo rauswieseln muss man lernen. Das unterscheidet uns nun mal von den Tieren. Das Wiesel ausgenommen.'),
('If my grandmother had wheels she would have been a bicycle',
'wenn meine grossmutter Raeder hätte, wäre sie ein Fahrrad sein'),
]
device = 'cuda' if torch.cuda.is_available() else 'cpu'
handler = HandleStrings(translations).to(device)
transformer = Transformer(len(handler.base), len(handler.target)).to(device)
optimiser = torch.optim.Adam(transformer.parameters(), 1e-5)
def categorical_crossentropy(y_pred, y_true):
return - torch.sum(y_true * torch.log(y_pred))
epochs = 500
losses = np.zeros(epochs)
n_sentences = len(handler)
with tqdm(total=epochs) as tq:
for i in range(epochs):
loss_epoch = 0
shuffle(handler)
for enc_in, dec_in, y_true, enc_mask, dec_mask in handler:
y_pred = transformer(enc_in, dec_in, enc_mask, dec_mask)
loss = categorical_crossentropy(y_pred, y_true)
loss.backward()
optimiser.step()
optimiser.zero_grad()
loss_epoch += loss.cpu().detach().numpy()
losses[i] = loss_epoch
tq.set_description(f'Loss:{losses[i]:.2f}')
tq.update(1)
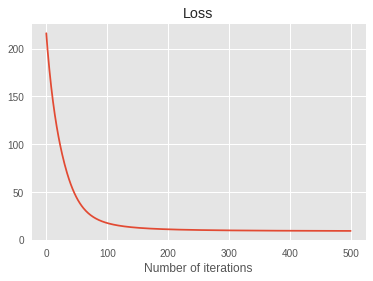
plt.plot(losses)
plt.title('Loss')
plt.xlabel('Number of iterations')
Loss:9.11: 100%|██████████| 500/500 [05:39<00:00, 1.48it/s]
Text(0.5, 0, 'Number of iterations')
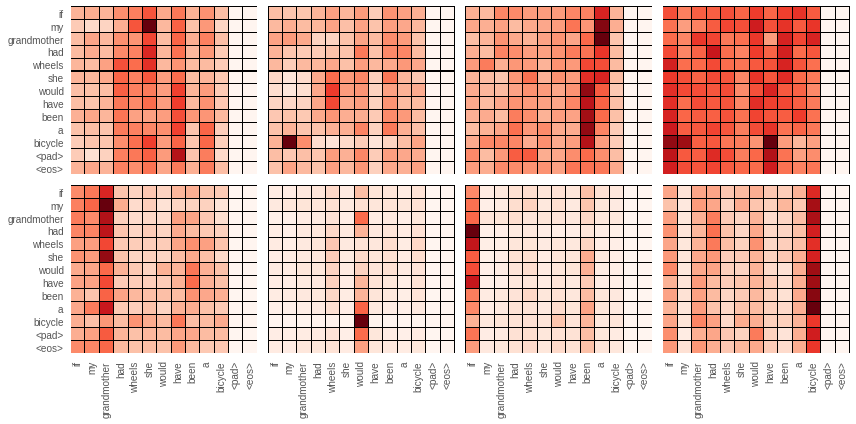
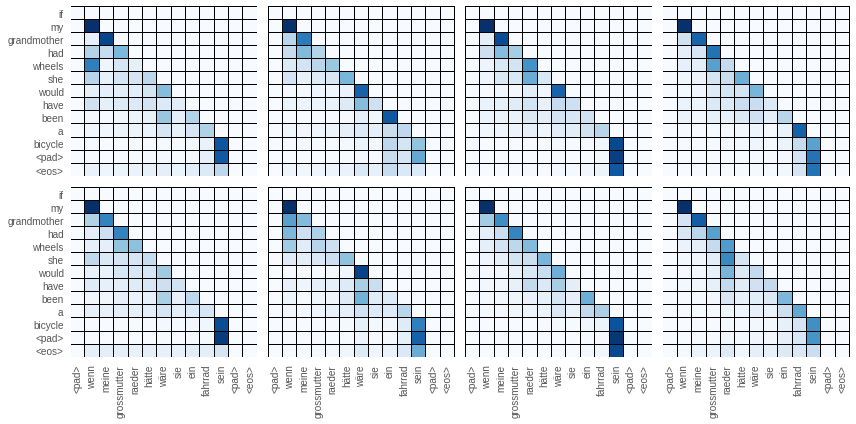
Below are the first layers attention networks both from the encoder and the decoder. From the decoder I plotted the special one which takes the encoder out as input. Although it is tempting to read these as justification for what the network is doing, this isn’t always true. The way to read these plots is looking row by row. Each row shows what the network is paying attention to when the word of that row is being translated. Because looking ahead in the decoder blocked, the decoder can only see to the left of the diagonal.
import pandas as pd
handler = HandleStrings(translations).to(device)
enc_in, dec_in, _, enc_mask, dec_mask = handler[-1]
enc_emb = transformer.encoder.input_enc(enc_in)
enc_out = transformer.encoder(enc_in, enc_mask)
dec_emb = transformer.decoder.input_enc(dec_in)
fig, ax = plt.subplots(figsize=(3 * 4, 3 * 2),
nrows=2,
ncols=4,
sharex=True,
sharey=True)
ax = ax.flat
for i in range(8):
weight_, _ = transformer.encoder.layers[0].attn.attns[i]._weight_value(enc_emb, enc_emb, enc_emb, enc_mask)
weight = weight_.cpu().detach().numpy()
df = pd.DataFrame(weight, index=handler.text[-1][0], columns=handler.text[-1][0])
sns.heatmap(df, annot=False, cmap='Reds', ax=ax[i], linecolor='black', linewidths=.01, cbar=False)
fig.tight_layout()
plt.show()
attn1_out = transformer.decoder.layers[0].attn1(dec_emb, dec_emb, dec_emb, dec_mask)
ln1_out = transformer.decoder.layers[0].ln1(attn1_out + dec_emb)
fig, ax = plt.subplots(figsize=(3 * 4, 3 * 2),
nrows=2,
ncols=4,
sharex=True,
sharey=True)
ax = ax.flat
for i in range(8):
weight_, _ = transformer.decoder.layers[0].attn2.attns[i]._weight_value(ln1_out,
enc_out,
enc_out,
dec_mask)
weight = weight_.cpu().detach().numpy()
df = pd.DataFrame(weight, index=handler.text[-1][0], columns=handler.text[-1][1])
sns.heatmap(df, annot=False, cmap='Blues', ax=ax[i], linecolor='black', linewidths=.01, cbar=False)
fig.tight_layout()
That’s it from me. Hope that was at least somewhat helpful in understanding how transformers work. If you are interested in playing around with transformers, I would recommend that you grab pre-trained BERT, which is a much better starting place than a untrained model.