FizzBuzz is one of the most well-known interview questions. The problem is stated as:
Write the numbers from 0 to n replacing any number divisible by 3 with Fizz, divisible by 5 by Buzz and divisible by both 3 and 5 by FizzBuzz. The example program should output 1, 2, Fizz, 3, Buzz, Fizz, 7, 8, Fizz, Buzz.
A while back, there was this infamous post where the author claimed to solve this problem in an interview using tensorflow. In this post I am going to do the same in pytorch but using neural arithmetic logic units (NALU) gates.

The paper is really interesting and I would definitely recommend reading it because my outline here probably isn’t going to do it justice. The idea behind NALU gates is that neural networks currently are really bad doing arithmetic operations. Even forgetting about arithmetic, neural networks really struggle with learning the identity. I will repeat the authors experiment here which consists of trying to fit the identity function:
import torch
from torch import nn
import torch.nn.functional as F
from tqdm import tqdm
import numpy as np
class NonLinearTest(nn.Module):
def __init__(self, non_linearity):
super().__init__()
activation = getattr(nn, non_linearity)
layers = [
nn.Linear(1, 8),
activation(),
nn.Linear(8, 8),
activation(),
nn.Linear(8, 8),
activation(),
nn.Linear(8, 8),
activation(),
nn.Linear(8, 1),
]
self.model = nn.Sequential(*layers)
def forward(self, x):
return self.model(x)
models = ['Sigmoid', 'ReLU', 'Tanh', 'ReLU6', 'CELU', 'SELU', 'ELU', 'LeakyReLU']
models = {x: NonLinearTest(x) for x in models}
optimisers = {name: torch.optim.Adam(model.parameters(), .001)
for name, model in models.items()}
epochs = 10000
X_train = np.linspace(-5, 5, 1000).reshape(-1, 1)
y_train = X_train
X_train, y_train = torch.Tensor(X_train), torch.Tensor(y_train)
for _ in tqdm(range(epochs)):
idx = perm = torch.randperm(1000)
for name, model in models.items():
y_pred = model(X_train[idx, :])
loss = torch.mean((y_pred - y_train[idx])**2)
loss.backward()
optimisers[name].step()
optimisers[name].zero_grad()
100%|██████████| 10000/10000 [02:28<00:00, 67.52it/s]
So we trained the network to fit the identity function using numbers between -5 and 5. When you zoom out and ask for predictions for numbers between -20 and 20, we can see an increase in mean absolute error:
import pandas as pd
X_test = np.linspace(-20, 20, 1000).reshape(-1, 1)
y_test = X_test
X_test, y_test = torch.Tensor(X_test), torch.Tensor(y_test)
tests = {name: torch.abs(model(X_test) - y_test).detach().numpy().reshape(-1)
for name, model in models.items()}
tests = pd.DataFrame(tests, index=np.linspace(-20, 20, 1000))
ax = tests.plot()
ax.legend(bbox_to_anchor=(1.01, 1.01), loc='upper left')
ax.set_ylabel('Mean absolute error')
Text(0, 0.5, 'Mean absolute error')
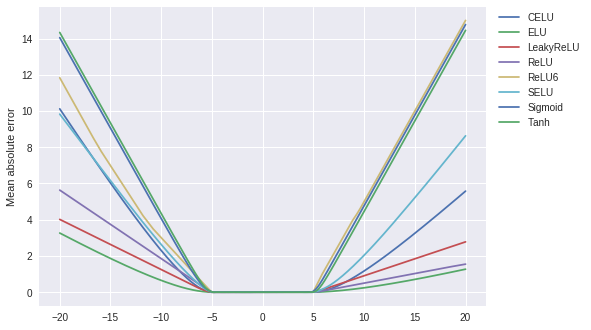
The network hasn’t really learned the identity function. The goal of NALU is to be able to replicate arithmetic operations. So how do we do this? Let’s focus on addition/substitution for now, we want something like this, $$ f_{\xi}(x_1, x_2) = (\xi_{1, 1} x_1 + \xi_{1, 2} x_2, \xi_{2, 1}x_1 + \xi_{2,2} x_2, …) $$ where $\xi_{i,j} \in {-1, 0,1}$ are parameters to be learned. This is not differentiable in $\xi$ and we can get around that by setting $$ \xi_{i,j} = \text{tanh}(u_{i, j})\text{sigmoid}(z_{i, j}) $$ where $u, v$ are the parameters to be fitted. You might be wondering at this point, why not just tanh since that can take the value 0. The range of values for tanh to stay near 0 is quite small so it becomes rather difficult to switch off any $\xi$ by using tanh alone.
On the multiplication/division, this just amount to transforming things into log-space $$ \begin{aligned} x_1 \cdot x_2 &= \exp(\log(x_1) + \log(x_2))\\ \frac{x_1}{x_2} &= \exp(\log(x_1) - \log(x_2)). \end{aligned} $$ We just need to be careful not to divide by zero, so typically one would just add a small number like $\epsilon = 10^{-10}$ to prevent this. Writing everything together gives the formulas which I have lifted out of the paper, $$ \begin{aligned} &\text{NAC: } \quad , , \mathbf{a}=\mathbf{Wx} && \mathbf{W}=\tanh(\mathbf{\hat{W}}) \odot \sigma(\mathbf{\hat{M}}) \\&\text{NALU:} \quad \mathbf{y} = \mathbf{g} \odot \mathbf{a} + (1-\mathbf{g}) \odot \mathbf{m} && \mathbf{m}=\exp \mathbf{W}(\log(|\mathbf{x}| + \epsilon)), ; \mathbf{g} = \sigma(\mathbf{Gx}). \end{aligned} $$ Here is my implementation in pytorch:
class NAC(nn.Module):
def __init__(self, d_in, d_out):
super().__init__()
self.hat_W = nn.Parameter(.1 * torch.randn((d_in, d_out)))
self.hat_M = nn.Parameter(.1 * torch.randn((d_in, d_out)))
def forward(self, x):
W = torch.tanh(self.hat_W) * torch.sigmoid(self.hat_M)
return x @ W
class NALU(nn.Module):
def __init__(self, d_in, d_out, eps=1e-10):
super().__init__()
self.nac_a = NAC(d_in, d_out)
self.G = nn.Parameter(.01 * torch.randn((d_in, d_out)))
self.nac_m = NAC(d_in, d_out)
self.eps = eps
def forward(self, x):
log_x = torch.log(torch.abs(x) + self.eps)
m = torch.exp(self.nac_m(log_x))
a = self.nac_a(x)
g = torch.sigmoid(x @ self.G)
return g * a + (1 - g) * m
Alright, so as I mentioned earlier, this seems to be quite a good candidate for doing FizzBuzz using neural networks.
import numpy as np
class FizzBuzzLearner(nn.Module):
def __init__(self, shape):
super().__init__()
layers = list()
for w_in, w_out in zip(shape[:-1], shape[1:]):
layers.append(NALU(w_in, w_out))
layers.append(nn.LogSoftmax(-1))
self.model = nn.Sequential(*layers)
def forward(self, x):
return self.model(x)
def fizz_buzz_category(x):
div_3 = x % 3 == 0
div_5 = x % 5 == 0
if div_3 and div_5:
return np.array([1, 0, 0, 0])
elif div_3:
return np.array([0, 1, 0, 0])
elif div_5:
return np.array([0, 0, 1, 0])
return np.array([0, 0, 0, 1])
def cat_to_fb(x, i):
return ['FizzBuzz', 'Fizz', 'Buzz', i][np.argmax(x)]
def fizz_buzz(x):
return cat_to_fb(fizz_buzz_category(x), x)
For the input, we give it the triplet $(i, 3, 5)$ where i is the number to be mapped to FizzBuzz. The network should use the 3 and the 5 to figure out what to do.
from tqdm import tqdm
from random import shuffle
import matplotlib.pyplot as plt
plt.style.use('ggplot')
device = 'cuda'
model = FizzBuzzLearner([3, 4096, 4]).to(device)
X = np.arange(100000).reshape(-1, 1)
X = np.pad(X, ((0,0), (0,1)), 'constant', constant_values=3)
X = np.pad(X, ((0,0), (0,1)), 'constant', constant_values=5)
y = np.array([fizz_buzz_category(x) for x in X[:, 0]])
X_train, y_train = X[:100, :], y[:100, :]
n = len(y_train)
X_train, y_train = torch.Tensor(X_train).to(device), torch.Tensor(y_train).to(device)
optimiser = torch.optim.Adam(model.parameters(), 1e-6)
epochs = 25000
losses = np.zeros(epochs)
accs = np.zeros(epochs)
batch_size = 512
N = X_train.shape[0]
with tqdm(total=epochs) as tq:
for i in range(epochs):
perm = torch.randperm(N)
loss_epoch = 0
acc = 0
for j in range(0, n, batch_size):
idx = perm[j:(j+batch_size)]
X_batch = X_train[idx, :]
y_batch = y_train[idx]
y_pred = model(X_batch)
loss = - torch.sum(y_batch * y_pred)
loss.backward()
optimiser.step()
optimiser.zero_grad()
loss_epoch += loss.cpu().detach().numpy()
acc += torch.sum(
torch.argmax(y_pred, -1) == torch.argmax(y_batch, -1)
).cpu().detach().numpy()
losses[i] = loss_epoch
accs[i] = 100 * acc / N
tq.set_description(f'Loss:{losses[i]:.2f} Acc:{accs[i]:.1f}%')
tq.update(1)
plt.plot(losses)
Loss:0.11 Acc:100.0%: 100%|██████████| 25000/25000 [03:55<00:00, 106.35it/s]
[<matplotlib.lines.Line2D at 0x7f286064da58>]
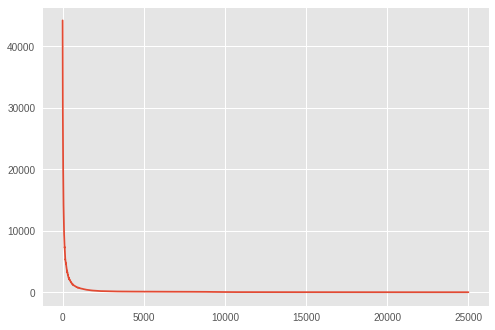
Pretty impressive, but did it actually learn the rule? The answer is a yes, we get the similar fantastic performance out of sample.
import pandas as pd
X_test, y_test = torch.Tensor(X[:100, :]).to(device), y[:100]
preds = np.exp(model(X_test).cpu().detach().numpy())
acc = np.mean(np.argmax(preds, axis=-1) == np.argmax(y_test, axis=-1))
print(f'OoS accuracy: {100 * acc:.1f}%')
pd.DataFrame([{'input': i, 'prediction': cat_to_fb(preds[i], i)} for i in range(20)])
OoS accuracy: 100.0%
| input | prediction | |
|---|---|---|
| 0 | 0 | FizzBuzz |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | Fizz |
| 4 | 4 | 4 |
| 5 | 5 | Buzz |
| 6 | 6 | Fizz |
| 7 | 7 | 7 |
| 8 | 8 | 8 |
| 9 | 9 | Fizz |
| 10 | 10 | Buzz |
| 11 | 11 | 11 |
| 12 | 12 | Fizz |
| 13 | 13 | 13 |
| 14 | 14 | 14 |
| 15 | 15 | FizzBuzz |
| 16 | 16 | 16 |
| 17 | 17 | 17 |
| 18 | 18 | Fizz |
| 19 | 19 | 19 |